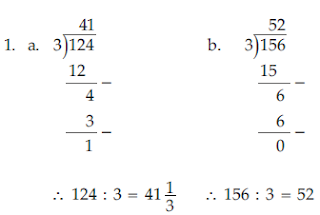smpmuhammadiyah1kapasansurabaya

smpmuhammadiyah1kapasansurabaya

smpmuhammadiyah1kapasansurabaya

Penjumlahan dan Pengurangan pada Pecahan

smpmuhammadiyah1kapasansurabaya

sumber: http://www.plengdut.com/2013/03/penjumlahan-dan-pengurangan-pada-pecahan.html

Operasi penjumlahan dan pengurangan pada pecahan mula-mula dilakukan dengan menentukan KPK dari penyebut-penyebutnya. Begitu pula halnya dengan operasi bentuk pecahan aljabar. Pertama-tama kita harus menentukan KPK dari penyebut-penyebut pecahan terlebih dahulu.

Perhatikan bentuk berikut:

a) KPK dari 12a dan 18b

b) KPK dari 4a²bc, 6ab²c², 8ab³c

Pada penjumlahan dan pengurangan bentuk pecahan aljabar, penyebut dari pecahan aljabar itu harus sama. Pecahan yang penyebutnya berbeda harus disamakan terlebih dahulu dengan cara mencari KPK dari penyebutpenyebutnya seperti cara menentukan KPK di atas.

Perhatikan contoh berikut ini.

Mengurutkan Pecahan

Perhatikan Gambar di bawah. Pada bagian A daerah yang diarsir mewakili 2/8 bagian lingkaran, sedangkan pada bagian B daerah yang diarsir mewakili 3/8 bagian lingkaran. Pada gambar tampak bahwa daerah B lebih luas dari daerah A. Berdasarkan kenyataan tersebut dapat kita katakan 3/8 lebih dari 2/8 atau 2/8 kurang dari 3/8 .

Pecahan

Untuk membandingkan dua nilai seperti gambar di samping, kita dapat menggunakan tanda “lebih dari” atau “kurang dari”. Contoh a > b (dibaca a lebih dari b), artinya nilai a lebih besar dari nilai b. Tanda b < a (dibaca b kurang dari a) artinya nilai b lebih kecil dari nilai a. Untuk membandingkan dua pecahan akan lebih mudah jika penyebutnya sama. Perhatikan contoh berikut.

Jika penyebut kedua pecahan itu tidak sama, maka langkah yang harus dilakukan adalah menyamakan penyebutnya terlebih dahulu. Misalnya untuk mengetahui hubungan lebih atau kurang dari kedua pecahan 1/2 dan 1/3, perhatikan contoh berikut ini.

Contoh Soal:

Berilah tanda > atau < pada pecahan berikut ini.
a. 1/3.....2/5
b.3/4.....2/3

Penyelesaian:
a. KPK dari 3 dan 5 adalah 15.

b. KPK dari 4 dan 3 adalah 12.

Untuk mengurutkan beberapa pecahan perlu diperhatikan penyebut dari pecahan tersebut. Penyebut yang sama memudahkan untuk mengurutkan beberapa pecahan.
 

Contoh:

Urut-urutan seperti pada contoh a di atas disebut urutan naik, sedangkan untuk contoh b disebut urutan turun. Untuk pecahan-pecahan yang tidak sama penyebutnya dalam mengurutkannya terlebih dahulu disamakan penyebutnya.  Perhatikan contoh soal berikut ini.

Urutkan pecahan berikut menurut urutan naik:
5/6, 2/3, 3/4.

Penyelesaian:
Untuk mengurutkan pecahan-pecahan tersebut terlebih dahulu kita tentukan KPK dari 6, 3, dan 4 yaitu 12.

Dari perhitungan tersebut, tampak bahwa urutannya adalah 8/12, 9/12, dan 10/12. Dengan demikian, urutan pecahannya adalah 2/3, 3/4, 5/6.

 

 

sumber: http://www.plengdut.com/2013/02/mengurutkan-pecahan.html

Pembagian Pada Bilangan Bulat

Pembagian

Misalnya pada suatu saat kalian ditanya, “Berapakah nilai a yang memenuhi persamaan 42 : 7 = a?” Dan pada saat yang lain kalian ditanya lagi, “Bilangan berapakah yang jika dikalikan dengan 7 menghasilkan bilangan 42?”

Dari dua contoh soal tadi, apakah keduanya memiliki jawaban yang sama? Kedua contoh soal di atas dapat disederhanakan bentuknya menjadi seperti berikut ini.

42 : 7 = a
a × 7 = 42

 

Ternyata nilai a yang memenuhi jawaban kedua pertanyaan di atas adalah 6. Apa yang dapat kamu simpulkan dari kedua bentuk pertanyaan tersebut?

Operasi pembagian bilangan bulat merupakan kebalikan dari operasi perkalian, sehingga dapat disimpulkan 

Jika a, b, dan c adalah bilangan bulat dan b ≠ 0 maka a : b = c jika dan hanya jika a = b × c.

Operasi pembagian dapat dinyatakan dalam beberapa bentuk.

Bentuk pembagian di atas dapat digunakan sesuai kebutuhan. Bentuk (a) digunakan untuk pembagian yang
sederhana, sedangkan bentuk (b) biasanya digunakan untuk pembagian yang rumit.

Ada beberapa istilah yang perlu diketahui dalam operasi pembagian bilangan bulat yaitu pembagi, bilangan yang dibagi, hasil bagi, dan sisa pembagian.

Contoh:

a. 12 : 3 = 4

12 disebut bilangan yang dibagi
3 disebut bilangan pembagi
4 disebut bilangan hasil bagi

b.

Hasil pembagian ini adalah

.

Contoh Soal

1. Hitunglah hasil pembagian berikut.
a. 124 : 3                    b. 156 : 3

2. Suatu bilangan dibagi dengan 4 hasilnya 15 dan sisanya 2. Tentukanlah bilangan yang dimaksud.

3. Suatu bilangan terdiri atas dua digit habis dibagi dengan 3. Jika dibagi dengan 5 sisanya 3. Tentukanlah bilangan itu.

Penyelesaian:

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Bilangan yang dimaksud adalah 4 × 15 + 2 = 62

3. Bilangan yang terdiri atas dua digit adalah bilangan puluhan. Bentuk bilangan tersebut adalah 10x + 3. Nilai x dicoba dari 1 hingga 9.

x = 1 → 10 × 1 + 3 = 13
x = 2 → 10 × 2 + 3 = 23
x = 3 → 10 × 3 + 3 = 33
x = 4 → 10 × 4 + 3 = 43
x = 5 → 10 × 5 + 3 = 53
x = 6 → 10 × 6 + 3 = 63
x = 7 → 10 × 7 + 3 = 73
x = 8 → 10 × 8 + 3 = 83
x = 9 → 10 × 9 + 3 = 93

Dari nilai di atas, bilangan yang habis dibagi 3 dan dibagi 5 bersisa 3 adalah 33, 63, dan 93.

 

Sifat Tanda pada Pembagian
Pada operasi pembagian bilangan bulat, tanda di depan bilangan yang dibagi perlu diperhatikan.

Contoh: 

36 : 4 = 9                                      
36 : (–4) = –9                              

–36 : 4 = –9

–36 : (–4) = 9

Apa yang dapat kalian simpulkan dari pola pembagian diatas? Diskusikan dengan teman-temanmu. 

 

 

 

sumber: http://www.plengdut.com/2013/02/pembagian.html

Perkalian Bilangan Bulat

Perkalian

Perhatikan Gambar susunan 6 buah apel (a). Diketahui terdapat tiga susun buah apel yang masing-masing susunnya terdiri atas dua apel yang saling sejajar. Perhatikan pula susunan 6 buah apel (b). Diketahui terdapat dua susun buah apel yang masingmasing susunnya terdiri atas tiga apel yang saling sejajar. Banyaknya buah apel pada susunan 6 buah apel (a) dan (b) masing-masing berjumlah (3 × 2) dan (2 × 3) buah.

Susunan 6 buah apel.
(a) susunan 3 × 2 buah apel
(b) susunan 2 × 3 buah apel

3 × 2 dan 2 × 3 merupakan salah satu bentuk operasi bilangan bulat yang disebut perkalian. Pada dasarnya, operasi perkalian bilangan bulat dapat dinyatakan dalam bentuk penjumlahan berulang.

Perhatikan contoh berikut.
3 × 2 = 2 + 2 + 2
2 × 3 = 3 + 3
5 × (–8) = (–8) + (–8) + (–8) + (–8) + (–8)

Sifat-Sifat Perkalian Bilangan Bulat
Untuk mengetahui sifat-sifat perkalian pada bilangan bulat, amati dan lengkapilah isian berikut.

1) Sifat komutatif
Apakah sifat komutatif berlaku pula pada perkalian bilangan bulat? Mari kita selidiki dengan menyalin dan melengkapi tabel di bawah ini.

Amatilah, ternyata bilangan pada kolom a × b sama dengan bilangan pada kolom ….
 

Jadi, dapat disimpulkan hal berikut.

Jika a dan b adalah bilangan bulat maka
a × b = … × …

2) Sifat asosiatif
Sifat asosiatif disebut juga sifat pengelompokan. Sifat asosiatif pada perkalian membolehkan kita untuk mengelompokkan bilangan-bilangan yang akan diselesaikan lebih dahulu.

Untuk menyelidiki apakah sifat asosiatif berlaku perkalian bilangan bulat, salin dan lengkapilah tabel berikut ini.

Amatilah, ternyata bilangan pada kolom (a × b) × c sama dengan bilangan pada kolom ....
 

Jadi, dapat disimpulkan hal berikut.

Jika a, b, dan c adalah bilangan bulat maka
(a × b) × c = … × (… × …)

3) Sifat distributif
Sifat distributif disebut juga sifat penyebaran. Perhatikan Gambar dibawah ini. Pada gambar tersebut banyaknya buah apel (6 × 2) dapat diuraikan menjadi (4 × 2) buah apel dan (2 × 2) buah apel.

Susunan (6 × 2) buah apel yang dibagi menjadi (4 × 2) dan (2 × 2) buah apel

Bentuk operasi ini disebut operasi distributif perkalian terhadap penjumlahan. Dari Gambar diatas dapat ditulis:

(4 + 2) × 2 = (4 × 2) + (2 × 2) atau 2 × (4 + 2) = (2 × 4) + (2 × 2)

Untuk lebih memahami sifat perkalian di atas, salin dan lengkapilah tabel berikut.

Amatilah, bilangan pada kolom a × (b + c) sama dengan bilangan pada kolom ....
 

Jadi, dapat simpulkan hal berikut.

Jika a, b, dan c adalah bilangan bulat maka
a × (b + c) = (… × …) + (… × …)

Dengan menggunakan cara yang sama seperti sebelumnya, coba kamu buktikan bahwa sifat distributif perkalian juga berlaku terhadap operasi pengurangan. Jika kamu teliti nanti akan dapat kamu buktikan bahwa untuk a, b, dan c adalah bilangan bulat maka berlaku sifat berikut.

Jika a, b, dan c adalah bilangan bulat maka
a × (b – c) = (a × b) – (a × c)

Sifat ini disbut sifat distributif perkalian terhadap pengurangan. Sifat distributif sering digunakan untuk mempermudah perhitungan seperti pada contoh berikut.

Contoh Soal:

1. Hitunglah operasi berikut ini.
23 × 17 + 23 × 83

Penyelesaian:
Bilangan yang sama ditulis di luar tanda kurung.

2. Hitunglah operasi berikut ini.
29 × 21 – 29 × 11
 

Penyelesaian:

4) Sifat identitas
Seperti halnya dengan operasi penjumlahan, pada operasi perkalian terdapat suatu bilangan yang jika dikalikan dengan bilangan tertentu akan menghasilkan bilangan itu sendiri. Dapatkah kalian mencari bilangan tersebut? Perhatikan contoh perkalian berikut ini.

5 × 1 = 5      0 × 1 = 0      –6 × 1 = –6

 

Dari ketiga contoh perkalian tersebut, ternyata jika suatu bilangan dikalikan dengan bilangan 1 akan menghasilkan bilangan itu sendiri. Dengan demikian, bilangan 1 adalah bilangan identitas atau unsur identitas dari operasi perkalian.

5) Sifat tertutup
Perhatikan operasi perkalian berikut.

2 × 3 = 6     –2 × 4 = –8     3 × –4 = –12

 

Bilangan-bilangan 2, 3, 4, –2, dan –4 pada operasi perkalian di atas merupakan bilangan bulat. Bilangan 6, –8, dan –12 merupakan hasil dari perkalian bilangan di atas.
 

Apakah bilangan-bilangan tersebut juga merupakan bilangan bulat? Tentu saja bilangan-bilangan 6, –8, dan –12 juga merupakan bilangan bulat. Dengan demikian, dapat kita simpulkan bahwa hasil kali bilangan-bilangan bulat akan menghasilkan bilangan bulat juga.

6) Sifat tanda pada perkalian
Dalam operasi perkalian bilangan bulat tanda di depan bilangan yang dikalikan perlu diperhatikan. Perhatikan contoh berikut ini.

12 × 12 = 144
12 × (–12) = –144
–12 × 12 = –144
–12 × (–12) = 144

Perhatikan pola perkalian di atas. Apa yang dapat kamu simpulkan? Dari uraian di atas, dapat disimpulkan hal berikut.

Bilangan bulat positif × bilangan bulat positif = bilangan bulat …
Bilangan bulat positif × bilangan bulat negatif = bilangan bulat …
Bilangan bulat negatif × bilangan bulat positif = bilangan bulat …
Bilangan bulat negatif × bilangan bulat negatif = bilangan bulat …

Contoh Soal:

Dengan menggunakan sifat-sifat operasi perkalian bilangan bulat, hitunglah perkalian-perkalian berikut ini.
a. 23 × 15 × 4 = ....
b. 24 × 15 + 24 × 85 = ....
c. 15 × 24 + 15 × 34 – 15 × 28 = ....
d. –6 × (–10) × (–6) × 25 = ....

Penyelesaian:
a. 23 × 15 × 4 = 23 × (15 × 4)
= 23 × 60
= 1.380

b. 24 × 15 + 24 × 85 = 24 × (15 + 85)
= 24 × 100
= 2.400

c. 15 × 24 + 15 × 34 – 15 × 28
= 15 × (24 + 34 – 28)
= 15 × (58 – 28) = 15 × 30 = 450

d. –6 × (–10) × (–6) × 25
= [–6 × (–10)] × [(–6) × 25]
= 60 × (–150)
= –9.000

 

 

 

sumber: http://www.plengdut.com/2013/02/perkalian.html

pengurangan bilangan bulat

Pengurangan

Misalkan kamu mempunyai sepuluh buah apel. Sebanyak dua buah apel kamu berikan kepada salah seorang temanmu. Berapakah sisa apel yang kamu miliki? Dengan mudah kamu akan menjawab sisa apel sebanyak = 10 – 2 = 8. Dalam matematika proses ini dinamakan pengurangan. Bentuk operasi pengurangan 10 – 2 dapat dihitung dengan cara menyusun ke bawah sebagai berikut:

10
2

— -
8

Sifat-Sifat Pengurangan Bilangan Bulat
1) Lawan suatu bilangan
Jika kalian perhatikan, ternyata himpunan bilangan bulat terdiri atas bilangan-bilangan yang berpasang-pasangan (seperti 5 dan –5, 2 dan –2, dan lain sebagainya). Bilangan –5 dikatakan lawan dari 5 dan bilangan 5 pun merupakan lawan dari –5. Secara umum jika a adalah suatu bilangan bulat maka –a merupakan lawan dari bilangan a. Jarak a dan –a dari titik 0 adalah sama namun arahnya berbeda.

Dari keterangan di atas dapat disimpulkan bahwa jika a adalah bilangan positif, maka –a adalah bilangan negatif. Jika b adalah bilangan negatif maka –b adalah bilangan positif. Perhatikan penjelasan berikut ini.

Jika a = 5 (bilangan positif) maka –a = –5 (bilangan negatif).
Jika b = –8 (bilangan negatif) maka –b = –(–8) = 8 (bilangan positif).

Contoh: 

2 – (–3) = 2 + 3 = 5
–2 – (–3) = –2 + 3 = 1
–2 – 3 = –5

Garis bilangan

2) Tanda kurung
Kita telah mempelajari operasi penjumlahan dan pengurangan secara terpisah pada bagian sebelumnya. Apabila kedua operasi tersebut digabungkan bagaimana cara mengerjakannya? Perhatikan contoh berikut.

Lakukan operasi pengurangan 27 – 12 terlebih dahulu mendapatkan hasil 15. Selanjutnya hasil 15 dijumlahkan dengan bilangan berikutnya (yaitu 52) mendapatkan hasil 67. Kemudian hasil 67 dikurangi dengan bilangan berikutnya (yaitu 42) mendapatkan hasil 25. Dengan demikian, hasil akhir operasi perhitungan di atas adalah 25. Dari contoh ini, dapatkah kamu mengambil sebuah kesimpulan?

Jika pada operasi gabungan penjumlahan dan pengurangan terdapat tanda kurung, pengerjaan operasi penjumlahan dan pengurangan itu tetap dikerjakan dari kiri kekanan dan operasi di dalam tanda kurung dikerjakan terlebih dahulu.

Contoh Soal:

1. Hitunglah soal berikut.
25 – 34 – [42 – (63 – 51)]

2. Hitunglah soal berikut.
16 – [(24 + 5) – 19] + 12

sumber: http://www.plengdut.com/2013/02/pengurangan.html

Penjumlahan Bilangan Bulat

Penjumlahan

Sewaktu di Sekolah Dasar kalian tentu telah mengenal operasi penjumlahan pada bilangan bulat, bukan? Untuk menyelesaikan operasi penjumlahan bilangan bulat dapat menggunakan mistar sederhana dan garis bilangan. Mistar yang digunakan memuat himpunan bilangan bulat. Untuk lebih jelasnya perhatikan contoh berikut ini.

Contoh Soal

Hitunglah –4 + 3 dengan menggunakan:
a. mistar sederhana;
b. garis bilangan.

Penyelesaian:
a. Menggunakan mistar sederhana

Langkah penyelesaiannya yaitu letakkan titik 0 pada mistar pertama tepat di atas angka –4 pada mistar kedua. Selanjutnya, lihat bilangan di bawah angka 3 pada mistar pertama sehingga pada mistar kedua diperoleh angka –1 sebagai hasilnya. Jadi, –4 + 3 = –1.

b. Menggunakan garis bilangan

Langkah penyelesaiannya yaitu sebagai berikut:
• dari titik nol melangkah ke kiri 4 satuan (karena negatif);
• kemudian dari titik –4 melangkah kekanan 3 satuan (karena positif).

Hasilnya adalah dari titik nol melangkah ke kiri 1 satuan atau sama dengan –1.
Jadi, –4 + 3 = –1.

Sebagai bahan latihan coba peragakan, bagaimana cara menyelesaikan penjumlahan –2 + (–7) menggunakan mistar sederhana? Jelaskan!

Jika kalian telah memahami konsep penjumlahan dengan garis bilangan, maka kalian dapat pula menentukan penjumlahan dua bilangan bulat dengan menggunakan pola tertentu seperti berikut ini.

1. 3 + (–4) = –4 + 3 = –(4 – 3)
                                = –1

 a + (–b) = –b + a = –(b – a)

2. 5 + 10 = 10 + 5 = 15

a + b = b + a

3. –7 + (–3) = –(7 + 3)
                   = –10

–a + (–b) = –(a + b)

Apakah kalian dapat menemukan cara lain yang lebih mudah dan cepat selain cara-cara di atas?

Selain bentuk penjumlahan di atas, operasi penjumlahan bilangan bulat juga dapat dilakukan dengan cara menyusun ke bawah seperti berikut ini.

Proses penjumlahan bilangan bulat dengan cara menyusun ke bawah lebih sering dipakai jika bilanganbilangan yang dijumlahkan cukup banyak.

Sifat-Sifat Penjumlahan Bilangan Bulat
Pada operasi penjumlahan bilangan bulat berlaku sifat-sifat yaitu komutatif, asosiatif, bilangan identitas, dan tertutup.

1) Sifat Komutatif
Salin dan isilah operasi penjumlahan berikut ini.

Buatlah kesimpulan dari hasil penjumlahan di atas. Bandingkanlah kesimpulanmu dengan teman yang lain. Kemudian, bandingkan pula dengan kesimpulan berikut.

Hasil penjumlahan bilangan bulat selalu sama walaupun letak bilangan ditukar. Sifat penjumlahan seperti ini disebut sifat komutatif dan ditulis:

a + b = b + a

2) Sifat Asosiatif
Coba kalian salin dan isi titik-titik pada operasi penjumlahan berikut dalam bukumu.

(33 + 37) + 7 = … + 7                       = … 

dan 

33 + (37 + 7) = 33 + …

                       = …

Berdasarkan hasil penjumlahan di atas, apakah (33 + 37) + 7 memiliki hasil yang sama dengan 33 + (37 + 7)? 

Setelah menjawab pertanyaan tadi, apa yang dapat kalian simpulkan mengenai kedua bentuk penjumlahan bilangan bulat tersebut? Diskusikan bersama temanmu dan bandingkan dengan kesimpulan berikut ini.

Pada operasi penjumlahan bilangan bulat, bilangan-bilangan tersebut dapat dikelompokkan dan ditulis dalam bentuk:

(a + b) + c = a + (b + c)

3) Bilangan identitas
Perhatikan penjumlahan bilangan bulat berikut.

3 + 0 = 3
–4 + 0 = –4
0 + (–5) = –5

Dari operasi penjumlahan di atas terlihat bahwa jika suatu bilangan bulat dijumlahkan dengan nol (0) selalu menghasilkan bilangan itu sendiri. Dalam matematika bilangan nol (0) disebut unsur identitas.

Penjumlahan bilangan bulat dengan unsur identitas ditulis:

a + 0 = 0 + a

4) Sifat tertutup
Perhatikan penjumlahan bilangan bulat berikut.

3 + 5 = 8     –2 + 6 = 4      –7 + 5 = –2

Bilangan-bilangan 3, 5, –2, 6, –7, dan 5 merupakan bilangan bulat. Bilangan-bilangan 8, 4, dan –2 merupakan hasil dari penjumlahan bilangan bulat. Apakah 8, 4, dan –2 juga merupakan bilangan bulat? Ya, bilangan 8, 4, dan –2 juga merupakan bilangan bulat. Dengan demikian dapat diambil kesimpulan sebagai berikut.

Penjumlahan bilangan bulat akan selalu menghasilkan bilangan bulat juga atau dapat ditulis jika a dan b ∈ B, maka a + b ∈ B. Sifat tertutup penjumlahan bilangan bulat: a + b = c; dengan a, b, dan c ∈ B.

sumber: http://www.plengdut.com/2013/02/penjumlahan.html

Pengertian Bilangan Bulat

Pernahkah kalian pergi ke kebun binatang? Hewan apa sajakah yang kalian lihat di sana? Tentu banyak sekali hewan-hewan yang dapat kalian lihat. Ada harimau, gajah, jerapah, dan hewan-hewan lainnya. Dapatkah kalian menghitung jumlah hewan-hewan tersebut? Misalkan jumlah harimau ada 20 ekor dan jumlah gajah ada 15 ekor. Bilangan 20 dan 15 yang kalian kenal merupakan contoh dari bilangan bulat. Ternyata dengan bilangan bulat kalian dapat menghitung apa saja yang ada di sekitar kita.

Gajah di kebun binatang

Selain dua contoh bilangan bulat yang disebutkan tadi, dalam matematika ada begitu banyak bilangan bulat yang jumlahnya tak terhingga. Bilangan apa sajakah yang termasuk dalam kelompok himpunan bilangan bulat?

a. Bilangan Bulat Positif, Bilangan Bulat Negatif, dan Nol
Dari kebun binatang, mari alihkan perhatian kita ke suatu tempat yang tinggi di permukaan bumi. Kita mengenal tempat tersebut sebagai daerah pegunungan. Bagaimanakah suhu udara di pegunungan? Tentunya dingin, bukan? Suhu udara menjadi semakin dingin ketika kita berada di puncak gunung yang tinggi. Suhu udara di pegunungan tinggi dan bersalju dapat mencapai 20 derajat Celsius di bawah nol. Dalam matematika, kuantitas 20 derajat Celsius di bawah nol ditulis/dinyatakan sebagai –20ºC dan dibaca negatif 20ºC.

Dari pegunungan, selanjutnya kita beralih ke laut. Misalkan ada seorang penyelam yang sedang berada 15meter di bawah permukaan laut. Dalam matematika, kuantitas 15 meter di bawah permukaan laut ditulis sebagai –15 meter dan dibaca negatif 15 meter. Bilangan-bilangan seperti 20, 15, –20, dan –15 memiliki besaran angka yang sama namun dengan tanda yang berbeda. Di dalam matematika, bilangan 20 dan 15 tergolong kelompok bilangan bulat positif sedangkan bilangan –20 dan –15 tergolong kelompok bilangan bulat negatif.

Di samping dua jenis bilangan bulat tersebut, terdapat satu bilangan bulat yang bukan bilangan negatif dan positif. Bilangan itu adalah nol (0), sehingga himpunan bilangan bulat terdiri atas bilangan bulat positif, bilangan bulat negatif, dan nol. Himpunan bilangan bulat dinotasikan dengan B = {..., –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, ...} dan dapat ditulis dalam garis bilangan seperti di bawah ini.

Garis bilangan bulat

b. Hubungan Antarbilangan Bulat
Perhatikan kembali Gambar Garis bilangan bulat diatas. Pada garis bilangan tersebut terlihat bahwa semakin ke kanan bilangannya semakin besar. Misalnya –1 dan 2. Bilangan 2 terletak di sebelah kanan bilangan –1 sehingga –1 kurang dari 2 atau ditulis –1 < 2. Sebaliknya, semakin ke kiri bilangannya semakin kecil. Misalnya –5 dan –2. Bilangan –5 terletak di sebelah kiri bilangan –2 sehingga –2 lebih dari –5 atau –2 > –5. Coba berikan contoh yang lain. Apakah hubungan tersebut berlaku untuk semua bilangan bulat, baik bilangan bulat positif, negatif, dan nol? Selidikilah!

 

sumber: http://www.plengdut.com/2013/02/pengertian-bilangan-bulat.html

Bilangan Bulat

Bilangan bulat terdiri dari bilangan cacah (0, 1, 2, 3, ...) dan negatifnya (-1, -2, -3, ...; -0 adalah sama dengan 0 sehingga tidak lagi dimasukkan secara terpisah). Bilangan bulat dapat dituliskan tanpa komponen desimal atau pecahan.
Himpunan semua bilangan bulat dalam matematika dilambangkan dengan Z (atau ), berasal dari Zahlen (bahasa Jerman untuk "bilangan").
Himpunan Z tertutup di bawah operasi penambahan dan perkalian. Artinya, jumlah dan hasil kali dua bilangan bulat juga bilangan bulat. Namun berbeda dengan bilangan asli, Z juga tertutup di bawah operasi pengurangan. Hasil pembagian dua bilangan bulat belum tentu bilangan bulat pula, karena itu Z tidak tertutup di bawah pembagian.

Bahasa Indah Matematika

Matematika selalu memberikan kesan 'angker' saat kita mendengarnya apalagi mempelajarinya. Tapi dibalik ke'angker'annya ternyata Matematika menyimpan sebuah keindahan. Perhatikan pola-pola perhitungan matematika berikut ini :

1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321

1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111

9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888

(0 x 9) + 8 = 8
(9 x 9) + 7 = 88
(98 x 9) + 6 = 888
(987 x 9) + 5 = 8888
(9876 x 9) + 4 = 88888
(98765 x 9) + 3 = 888888
(987654 x 9) + 2 = 8888888
(9876543 x 9) + 1 = 88888888
(98765432 x 9) + 0 = 888888888
(987654321 x 9) - 1 = 8888888888

3 x 37 = 111
6 x 37 = 222
9 x 37 = 333
12 x 37= 444
15 x 37 = 555
18 x 37 = 666
21 x 37 = 777

24 x 37 = 888
27 x 37 = 999

1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321



1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321

Matematika adalah sebuah Kebenaran. Tidak akan ada yang bisa menyangkal hasilnya. Juga salah satu keindahan yang datang dari Allah swt.

Sumber: milis immpas-itb
++++++++++++ +++++++++ +++++++++ +++++++++ +++++++++ +++++++++ ++

Alam ini selalu bertasbih kepada-Nya
Alam ini dirancang dengan begitu teliti & indahnya
Alam ini selalu harmonis dengan interaksi-interaksi nya
Alam ini selalu membentuk formasi yg tak menyalahi aturan-Nya
Alam ini dinyatakan dengan Bahasa Matematika untuk keUniversalannya
Alam ini kita di dalamnya, akankah kita katakan bahasa ini terjadi sendirinya?

Cara Melukis Sudut Istimewa

Tentu kalian sudah bisa menggambar sudut dengan menggunakan busur derajat. Bagaimanakah caranya menggambarkan sudut-sudut istimewa 30°, 45°, 60°, 90°, 135°, 180°, dan 270° dengan menggunakan jangka? Untuk memahami caranya, perhatikan uraian berikut ini.

a. Cara Melukis Sudut 90°, 60°, 45°, dan 30°

1) Cara Melukis Sudut 90° (perhatikan Gambar berikut)

Melukis sudut 90°

a) Buatlah garis g dari titik A.
b) Dari titik A dibuat busur dengan ukuran tertentu yang memotong garis g di B dan C.
c) Dari B dan C dibuat busur lingkaran yang berjari-jari sama dan kedua busur berpotongan di D.
d) Dari titik A tarik garis melalui D, maka terbentuk AD ⊥ BC dan ∠BAD = 90°.
 

2) Cara Melukis Sudut 60° (perhatikan Gambar berikut)

Melukis sudut 60°

a) Buatlah garis g dengan titik A terletak pada garis g.
b) Dari A buat busur lingkaran, memotong garis g di B.
c) Dari B dibuat busur lingkaran dengan jari-jari AB.
d) Kedua busur berpotongan di C.
e) Tarik dari titik A garis lurus melalui titik C.
f) ∠CAB adalah 60°.

3) Cara Melukis Sudut 45° (perhatikan Gambar berikut ini)

Melukis sudut 45°

Diketahui garis g yang melalui titik A. Kemudian dari A dibuat sudut 45°.
a) Buatlah sudut 90°.
b) Dari titik C dan D buatlah busur dengan jari-jari yang sama dan kedua busur berpotongan di F.
c) Tariklah garis dari titik A lewat F sehingga ∠FAC = 45°.

4) Cara Melukis Sudut 30° (perhatikan Gambar berikut ini)

Melukis sudut 30°

Diketahui garis g dengan titik A. Kemudian dari titik A dibuat sudut 30°.
a) Buatlah sudut 60° (lihat cara membuat sudut 60°).
b) Dari titik B dan C buat busur dengan jari-jari sama dan kedua busur berpotongan di D.
c) Dari A tarik garis lewat D sehingga besar ∠BAD = 30°.

b. Cara Melukis Sudut 120°, 135°, 180°, dan 270°

1) Cara Melukis Sudut 120°

Melukis sudut 120° dapat dikerjakan dengan mengikuti langkah-langkah melukis sudut 60°. Setelah sudut 60° terlukis yaitu ∠CAB maka terbentuklah ∠DAC = 120°. Mengapa ∠DAC = 120°? Berikan alasanmu.

Melukis sudut 120°

 

2) Cara Melukis Sudut 135°

Melukis sudut 135° dapat dilakukan dengan terlebih dahulu melukis sudut 45°. Setelah sudut 45° terlukis, yaitu ∠BAC = 45° maka terbentuklah ∠DAC = 135°. Mengapa demikian? Karena ∠BAC dan ∠DAC saling berpelurus.

Melukis sudut 135°

3) Cara Melukis Sudut 180°

Sudut 180° disebut juga sudut lurus. ∠AOB = 180°

∠AOB = 180°

4) Cara Melukis Sudut 270°

Untuk melukis sudut 270° dapat dikerjakan dengan melukis sudut 90°, terlebih dahulu. Setelah sudut 90° terlukis, yaitu ∠CAB = 90° maka terbentuklah ∠270°.

Melukis sudut 270°

 

sumber: www.plengdut.com/2013/03/cara-melukis-sudut-istimewa.html

Cara melukis garis istimewa

Suatu segitiga, di samping memiliki garis-garis sisi ternyata juga memiliki garis-garis lain. Garis-garis itu adalah garis tinggi, garis bagi, garis berat, dan garis sumbu. Di manakah garis-garis itu berada dalam suatu segitiga? Bagaimanakah cara melukisnya? Pada bagian ini kalian akan mempelajari garis-garis tersebut beserta cara melukisnya.

a. Cara Melukis Garis Tinggi

Garis tinggi adalah sebuah garis yang ditarik dari titik sudut suatu segitiga dan tegak lurus sisi di hadapannya. Untuk melukis garis tinggi suatu segitiga dapat dilakukan dengan cara sebagai berikut.

• Langkah 1. Buatlah segitiga ABC.
• Langkah 2. Dari titik sudut C, buatlah busur lingkaran dengan jari-jari r. Busur tersebut memotong sisi AB di titik D dan E.
• Langkah 3. Dari titik D dan E, buatlah busur lingkaran dengan jari-jari r (sama dengan busur lingkaran pada langkah 2). Kedua busur akan berpotongan di titik F.
• Langkah 4. Hubungkan titik C ke titik F dan CF merupakan garis tinggi segitiga ABC.

Melukis garis tinggi

Pada Gambar diatas terlihat garis tinggi CF yang dilukis berdasarkan langkah-langkah di atas. Dapatkah kalian membuat garis tinggi yang lain yang di mulai dari titik A atau B pada segitiga ABC tersebut?

b. Cara Melukis Garis Bagi

Garis bagi adalah suatu garis yang ditarik dari titik sudut segitiga dan membagi sudut itu menjadi dua bagian yang sama besar. Untuk melukis garis bagi dapat dilakukan dengan cara sebagai berikut. Langkah-langkah melukis garis bagi segitiga adalah sebagai berikut.

• Langkah 1. Buatlah segitiga ABC.
• Langkah 2. Buatlah busur lingkaran dengan titik A sebagai titik pusat. Busur tersebut akan memotong sisi AB dan AC berturut-turut di titik D dan E.
• Langkah 3. Buatlah busur lingkaran yang sama dengan busur lingkaran pada langkah 2 dengan titik D dan E sebagai titik pusatnya. Kedua busur lingkaran berpotongan di titik F.
• Langkah 4. Hubungkan titik A ke titik F. Garis AF yang terbentuk merupakan garis bagi segitiga.

Melukis garis bagi

Pada Gambar terlihat garis AF sebagai garis bagi suatu segitiga ABC, berdasarkan langkah-langkah di atas. Dapatkah kalian mencari garis bagi-garis bagi yang lainnya dari ΔABC tersebut? 

c. Cara Melukis Garis Berat dan Garis Sumbu Segitiga

Garis berat adalah garis yang ditarik dari titik sudut suatu segitiga ke pertengahan sisi dihadapannya. Garis sumbu adalah suatu garis yang ditarik dari tengah-tengah sisi suatu segitiga dan tegak lurus sisi tersebut. Untuk menggambar garis berat dan garis bagi suatu segitiga perhatikan langkahlangkah berikut.

• Langkah 1. Buatlah segitiga ABC.
• Langkah 2. Buatlah busur lingkaran dengan pusat titik B dengan jari-jari r.
• Langkah 3. Buatlah busur lingkaran dengan titik pusat C dengan jari-jari r.
• Langkah 4. Kedua busur yang dibentuk pada langkah 2 dan 3 akan berpotongan di titik D dan E.
• Langkah 5. Hubungkan titik D dan E, garis hubung DE disebut garis sumbu segitiga.
• Langkah 6. Garis gabung DE pada langkah 5 memotong sisi BC di F, lalu hubungkan titik A ke titik F. Garis AF yang terbentuk merupakan garis berat segitiga.

Garis berat segitiga dengan langkah-langkah di atas dapat dilihat pada Gambar berikut. 

Melukis garis berat

Sedangkan pada garis sumbu dapat dilihat pada Gambar berikut. 

Melukis garis sumbu

 

 

sumber:  www.plengdut.com/2013/03/cara-melukis-garis-istimewa