SIFAT-SIFAT SEGITIGA

SIFAT-SIFAT SEGITIGA

1. Segitiga Siku-Siku

Segitiga siku-siku dapat dibentuk dari sebuah persegi panjang dengan menarik salah satu garis diagonalnya.

Perhatikan gambar berikut:

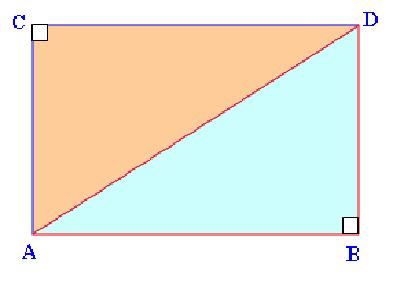
Bidang ABCD adalah persegi panjang. Dengan menarik diagonal AC, akan terbentuk dua segitiga siku-siku yang sama dan sebangun (konruen) yaitu ΔABC dan ΔADC.

Segitiga siku-siku mempunyai dua sisi siku-siku yang mengapit sudut siku-siku dan satu sisi miring (hypotenusa)

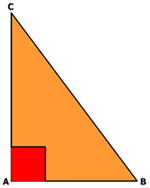
ΔABC mempunyai ciri-ciri:

AB dan BC sebagai sisi siku-siku, AC sebagai hypotenusa dan sudut ABC atau sudut B adalah sudut siku-siku (= 90°)

Dalam sebuah segitiga siku-siku, hypotenusa selalu terletak di depan sudut siku-siku.

2. Segitiga Sama Kaki

Dua buah segitiga siku-siku yang kongruen dapat membentuk sebuah segitiga sama kaki dengan mengimpitkan salah satu sisi siku-siku yang sama panjang dari kedua segitiga tersebut.

Perhatikan gambar berikut:

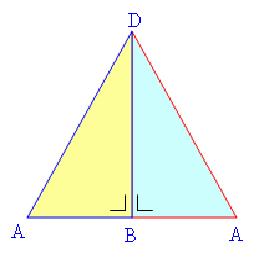
ΔABD dan ΔDBC adalah dua segitiga siku-siku yang kongruen. Sisi BD adalah sisi siku-siku yang sama panjang dari kedua segitiga tersebut. Jadi ΔACD adalah segitiga sama kaki dengan sisi AD=DC.

Di dalam segitiga sama kaki terdapat :

• Dua sisi yang sama panjang, sisi tersebut sering disebut kaki segitiga.
• Dua sudut yang sama besar yaitu sudut yang berhadapan dengan sisi yang panjangnya sama.
• Satu sumbu simetri.

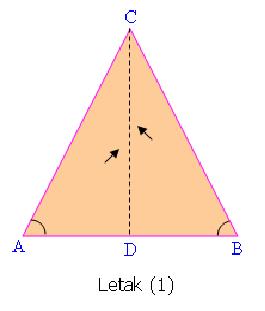
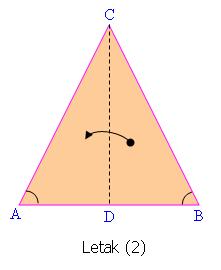
Segitiga sama kaki merupakan bangun simetri lipat dan dapat menempati bingkainya dalam dua cara.

Dari gambar disamping terlihat bahwa :

1. CD sebagai sumbu simetri
2. A pindah ke B; B pindah ke A dan C tetap.
3. AC pindah ke BC, maka AC=BC.
4. CAB pindah ke  ABC maka  CAB =  ABC

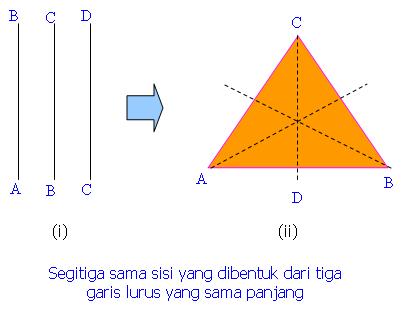
3. Segitiga Sama Sisi

Tiga buah garis lurus yang sama panjang dapt membentuk sebuah segitiga sama sisi dengan cara mempertemukan setiap ujung garis satu sama lainnya.

Gambar (i) di atas menunjukkan gambar tiga garis lurus yang sama panjang, yaitu AB= BC=CA. Apabila ujung-ujung ketiga garis tersebut saling dipertemukan, A dengan A, B dengan B, dan C dengan C, maka akan terbentuk segitiga sama sisi ABC seperti terlihat pada gambar (ii) di atas

Di dalam segitiga sama sisi terdapat :

1. Tiga sisi yang sama panjang.
2. Tiga sudut yang sama besar.
3. Tiga sumbu simetri.

sumber:http://segitigasmp.wordpress.com/sifat-sifat-segitiga/

Irisan Himpunan

Irisan dari dua himpunan A dan B adalah himpunan yang anggota-anggotanya ada di himpunan A dan ada di himpunan B. Dengan kata lain, himpunan yang anggotanya ada di kedua himpunan tersebut.

Contoh: A = {a, b, c, d, e} dan B = {b, c, f, g, h}

Pada kedua himpunan tersebut ada dua anggota yang sama yaitu b dan c. Oleh karena itu, dapat dikatakan bahwa irisan himpunan A dan B adalah b dan c atau ditulis dengan:

A ∩ B = {b, c}

A ∩ B dibaca himpunan A irisan himpunan B. Dengan diagram Venn A ∩ B dapat dinyatakan seperti pada Gambar berikut ini.

Daerah irisan A dan B.

Contoh Soal:

1. Diketahui: A= {1, 2, 3, 4, 5}
B = {2, 3, 6, 7, 8}
C = {4, 5, 6, 7, 8}
Tentukanlah:
a. A ∩ B         c. B ∩ C
b. A ∩ C        d. A ∩ B ∩ C

Penyelesaian:
a. A ∩ B = {2, 3}       c. B ∩ C = {6, 7, 8}
b. A ∩ C = {4, 5}      d. A ∩ B ∩ C = { }

2. Perhatikan gambar berikut.

Tentukanlah:
a. A                 e. n(A)
b. B                 f. n(B)
c. A ∩ B         g. n(A ∩ B)
d. S                 h. n(S)

 Penyelesaian:
a. A = {1, 2, 3, 4, 5}
b. B = {4, 5, 6, 7, 8}
c. A ∩ B = {4, 5}
d. S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
e. n(A) = 5

f. n(B) = 5
g. n(A ∩ B) = 2
h. n(S) = 11

sumber: http://www.plengdut.com/2013/03/

Jenis-Jenis Sudut

Besar suatu sudut dapat diukur dengan menggunakan busur derajat. Besar sudut yang dapat diukur adalah lebih dari 0° dan kurang dari 360°. Besar sudut-sudut dapat dibedakan seperti sudut lancip, sudut tumpul, sudut siku-siku, sudut lurus, dan sudut refleks.

a. Sudut Lancip

Sudut lancip adalah sudut yang besarnya kurang dari 90°.

Sudut lancip

 

b. Sudut Siku-Siku

Sudut siku-siku adalah sudut yang besarnya 90°. Sudut sikusiku biasa dinotasikan dengan ∟

Sudut siku-siku

 c. Sudut Tumpul

Sudut tumpul adalah sudut yang besarnya lebih dari 90° dan kurang dari 180°.

Sudut tumpul

d. Sudut Lurus

Sudut lurus adalah sudut yang besarnya 180°.

∠AOB sudut lurus

e. Sudut Refleks

Sudut refleks adalah sudut yang besarnya lebih dari 180° dan kurang dari 360°.

∠AOB sudut refleks

sumber:

http://www.plengdut.com/2013/03/jenis-jenis-sudut.html

Himpunan Bagian

Dalam matematika, terutama teori himpunan, suatu himpunan A adalah himpunan bagian dari himpunan B bila A "termuat" di dalam B. A dan B boleh jadi merupakan himpunan yang sama. Hubungan suatu himpunan yang menjadi himpunan bagian yang lain disebut sebagai "termasuk ke dalam" atau kadang-kadang "pemuatan". Himpunan B adalah superhimpunan dari A karena semua elemen A juga adalah elemen B.

sumber wikipedia






Diagram Venn menunjukkan A adalah himpunan bagian B and sebaliknya B adalah superhimpunan A

Segitiga Pascal untuk Himpunan bagian

Soal : Tentukan banyaknya himpunan bagian dari himpunan B = {a, b, c, d} yang memiliki 3 anggota!
Penyelesaian :
Permasalahan matematika di atas dapat kita selesaikan dengan menggunakan Segitiga Pascal. Sebenarnya ada “rumus cepat” untuk menyelesaikan permasalahan di atas. Namun, matematika bukanlah ilmu hapalan, jika anak kita ajak menghapal rumus matematika, itu tidak akan bertahan lama. Jadi, dengan Segitiga Pascal yang bentuk dan komposisinya menarik dan unik, diharapkan anak dapat menyelesaikan tipe permasalahan di atas, walaupun diberikan angka yg berbeda. Okay, mari lihat bagaimana Segitiga Pascal bekerja.
Segitiga Pascal

Yang belum paham cara membuat komposisi angka-angka di atas, silakan komen ya.
Himpunan B = {a, b, c, d} memiliki 4 anggota, pilih baris n = 4 pada Segitiga Pascal,
yaitu : 1 4 6 4 1
Makna dari masing-masing bilangan ini adalah :
1 = banyak himpunan bagian yang memiliki 0 anggota
4 = banyak himpunan bagian yang memiliki 1 anggota
6 = banyak himpunan bagian yang memiliki 2 anggota
4 = banyak himpunan bagian yang memiliki 3 anggota
1 = banyak himpunan bagian yang memiliki 4 anggota
Jadi, banyaknya himpunan bagian dari himpunan B = {a, b, c, d} yang memiliki 3 anggota ada 4 buah, yang jika kita jabarkan yaitu {a, b, c}, {a, b, d}, {a, c, d}, dan {b, c, d}

Sumber:http://yanatamath.wordpress.com/2012/12/15/menentukan-banyaknya-himpunan-bagian-dengan-segitiga-pascal/

Irisan dan Gabungan Dua Himpunan

Irisan himpunan A dan B adalah suatu himpunan yang anggotanya merupakan anggota himpunan A dan sekaligus merupakan anggota himpunan B.

Gabungan himpunan A dan B adalah suatu himpunan yang anggota-anggotanya merupakan anggota A saja, anggota B saja, dan anggota persekutuan A dan B.

Hubungan Sudut-Sudut pada Dua Garis Sejajar

a. Sudut-Sudut Sehadap

Garis a dan b sejajar dipotong oleh garis l, maka ∠A1 dan ∠B2 adalah sudut-sudut sehadap. Perhatikan Gambar dibawah ini. Apakah benar ∠A1 = ∠B2?

Sudut-sudut sehadap yang sama besar.

Untuk membuktikan kebenaran ∠A1 = ∠B2, lakukanlah kegiatan berikut ini. Jiplak atau salin ∠A1 pada Gambar diatas, kemudian guntinglah! Letakan ∠A1 hasil guntingan tadi pada ∠B2. Apakah ∠A1 dan ∠B2 berimpit dengan tepat? Dengan demikian, terbukti ∠A1 = ∠ .... Selanjutnya, lakukanlah hal seperti di atas untuk ∠A2, ∠A3, dan ∠A4.

Dari hasil kegiatan di atas dapat disimpulkan hal berikut.

Besar sudut-sudut yang sehadap adalah …

b. Sudut Dalam Berseberangan

Garis a dan b sejajar yang dipotong oleh garis l maka ∠A2 dan ∠B3 adalah sudut-sudut dalam berseberangan. Buktikanlah bahwa ∠A2 = ∠B3. Perhatikan Gambar dibawah ini.
Bukti: ∠A1 = ∠A2 (bertolak belakang) dan
∠A1 = ∠B3 (sehadap), maka
∠A2 = ∠B3 (terbukti)

Besar sudut dalam berseberangan sama

Sudut-sudut dalam
yang berseberangan sama besar.

c. Sudut Luar Berseberangan

Garis a dan b sejajar yang dipotong oleh garis l, maka ∠A1 dan ∠B3 adalah sudut-sudut luar berseberangan. Buktikanlah bahwa ∠A1 = ∠B3. Perhatikan Gambar dibawah ini.
Bukti: ∠A2 = ∠A1 (bertolak belakang)
∠A2 = ∠B3 (sehadap)
∠A1 = ∠B3 (terbukti)

Besar sudut luar berseberangan sama

Hubungan sudutsudut
luar berseberangan.

d. Sudut Dalam Sepihak

Garis a sejajar b dipotong oleh garis l maka ∠A2 dan ∠B3 adalah sudut dalam sepihak. Perhatikan Gambar dibawah ini. Buktikanlah bahwa ∠A2 + ∠B3 = 180°.
Bukti: ∠A1 = ∠B3 (sehadap) dan
∠A1 + ∠A2 = 180° (saling berpelurus), maka:
∠B3 + ∠A2 = 180° (terbukti)

Jumlah sudut dalam sepihak adalah 180°

Hubungan sudutsudut
dalam sepihak.

e. Sudut Luar Sepihak

Garis a sejajar b dipotong oleh garis l, ∠A2 dan ∠B3 adalah sudut luar sepihak. Perhatikan Gambar dibawah ini. Buktikan bahwa ∠A1 + ∠B3 = 180°.
Bukti: ∠A2 = ∠B3 (sehadap) dan
∠A1 + ∠A2 = 180° (saling berpelurus), maka
∠A1 + ∠B3 = 180° (terbukti)

Jumlah sudut luar sepihak adalah 180°

Hubungan
sudut-sudut luar sepihak

sumber: http://www.plengdut.com/2013/03/Hubungan-Sudut-Sudut-pada-Dua-Garis-Sejajar.html