Cara melukis garis istimewa

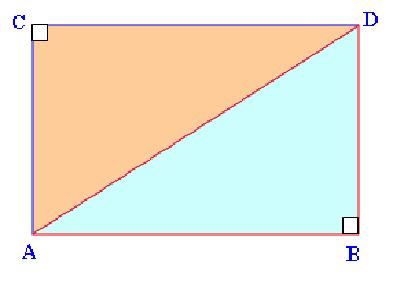
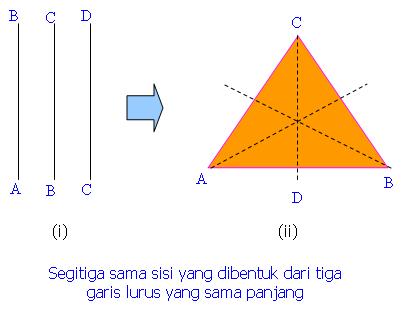
Suatu segitiga, di samping memiliki garis-garis sisi ternyata juga memiliki garis-garis lain. Garis-garis itu adalah garis tinggi, garis bagi, garis berat, dan garis sumbu. Di manakah garis-garis itu berada dalam suatu segitiga? Bagaimanakah cara melukisnya? Pada bagian ini kalian akan mempelajari garis-garis tersebut beserta cara melukisnya.

a. Cara Melukis Garis Tinggi

Garis tinggi adalah sebuah garis yang ditarik dari titik sudut suatu segitiga dan tegak lurus sisi di hadapannya. Untuk melukis garis tinggi suatu segitiga dapat dilakukan dengan cara sebagai berikut.

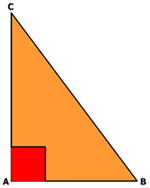
• Langkah 1. Buatlah segitiga ABC.
• Langkah 2. Dari titik sudut C, buatlah busur lingkaran dengan jari-jari r. Busur tersebut memotong sisi AB di titik D dan E.
• Langkah 3. Dari titik D dan E, buatlah busur lingkaran dengan jari-jari r (sama dengan busur lingkaran pada langkah 2). Kedua busur akan berpotongan di titik F.
• Langkah 4. Hubungkan titik C ke titik F dan CF merupakan garis tinggi segitiga ABC.

Melukis garis tinggi

Pada Gambar diatas terlihat garis tinggi CF yang dilukis berdasarkan langkah-langkah di atas. Dapatkah kalian membuat garis tinggi yang lain yang di mulai dari titik A atau B pada segitiga ABC tersebut?

b. Cara Melukis Garis Bagi

Garis bagi adalah suatu garis yang ditarik dari titik sudut segitiga dan membagi sudut itu menjadi dua bagian yang sama besar. Untuk melukis garis bagi dapat dilakukan dengan cara sebagai berikut. Langkah-langkah melukis garis bagi segitiga adalah sebagai berikut.

• Langkah 1. Buatlah segitiga ABC.
• Langkah 2. Buatlah busur lingkaran dengan titik A sebagai titik pusat. Busur tersebut akan memotong sisi AB dan AC berturut-turut di titik D dan E.
• Langkah 3. Buatlah busur lingkaran yang sama dengan busur lingkaran pada langkah 2 dengan titik D dan E sebagai titik pusatnya. Kedua busur lingkaran berpotongan di titik F.
• Langkah 4. Hubungkan titik A ke titik F. Garis AF yang terbentuk merupakan garis bagi segitiga.

Melukis garis bagi

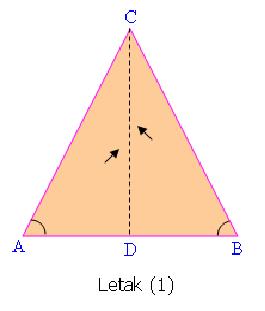
Pada Gambar terlihat garis AF sebagai garis bagi suatu segitiga ABC, berdasarkan langkah-langkah di atas. Dapatkah kalian mencari garis bagi-garis bagi yang lainnya dari ΔABC tersebut? 

c. Cara Melukis Garis Berat dan Garis Sumbu Segitiga

Garis berat adalah garis yang ditarik dari titik sudut suatu segitiga ke pertengahan sisi dihadapannya. Garis sumbu adalah suatu garis yang ditarik dari tengah-tengah sisi suatu segitiga dan tegak lurus sisi tersebut. Untuk menggambar garis berat dan garis bagi suatu segitiga perhatikan langkahlangkah berikut.

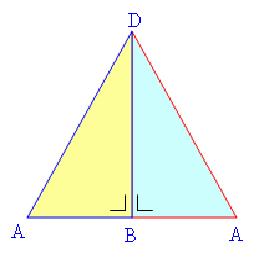
• Langkah 1. Buatlah segitiga ABC.
• Langkah 2. Buatlah busur lingkaran dengan pusat titik B dengan jari-jari r.
• Langkah 3. Buatlah busur lingkaran dengan titik pusat C dengan jari-jari r.
• Langkah 4. Kedua busur yang dibentuk pada langkah 2 dan 3 akan berpotongan di titik D dan E.
• Langkah 5. Hubungkan titik D dan E, garis hubung DE disebut garis sumbu segitiga.
• Langkah 6. Garis gabung DE pada langkah 5 memotong sisi BC di F, lalu hubungkan titik A ke titik F. Garis AF yang terbentuk merupakan garis berat segitiga.

Garis berat segitiga dengan langkah-langkah di atas dapat dilihat pada Gambar berikut. 

Melukis garis berat

Sedangkan pada garis sumbu dapat dilihat pada Gambar berikut. 

Melukis garis sumbu

 

 

sumber:  www.plengdut.com/2013/03/cara-melukis-garis-istimewa

Keliling dan Luas Trapesium

Coba kalian perhatikan Gambar berikut ini.

Trapesium ABCD

Gambar tersebut merupakan sebuah trapesium dengan sisi-sisi, yaitu a, b, c, dan d. Keliling trapesium ABCD diatas = AB + BC + CD + DA
= b + d + a + c

Keliling trapesium = b + d + a + c

Untuk mencari luas trapesium, lakukan kegiatan berikut.

1. Jiplaklah trapesium ABCD pada Gambar trapesium diatas. Kemudianbuatlah satu buah trapesium yang kongruen dengan trapesium ABCD.

2. Hubungkan sisi miring trapesium tersebut sehingga terbentuk persegi panjang. Apakah hasil yang kalian dapatkan seperti pada gambar di bawah ini?

Dari gambar itu, tentu kalian tahu bahwa BE = DC = a dan CF = AB = b, sehingga luas persegi panjang AEFD = AE × AD = (… + …) × AD

3. Luas trapesium ABCD = ½ Luas persegi panjang AEFD
= ½ (… + …) × …

dengan AD = t adalah garis tinggi trapesium, maka akan kita dapatkan.
Luas trapesium = ½ (… + …) × …

Contoh Soal:

Pada gambar berikut, ABCD adalah trapesium sama kaki dengan AD = BC = DC = 10 cm, DE = 8 cm, dan AB = 2 × DC. Hitunglah keliling dan luasnya.

Penyelesaian:
AD = BC = DC = 10 cm
AB = 2 × DC = 2 × 10 cm = 20 cm

Keliling = AB + BC + DC + AD
= 20 + 10 + 10 + 10 = 50 cm

Luas = ½ (10 + 20) x 8 = 30 × 4 = 120 cm²

Keliling dan Luas Jajar Genjang

Gambar dibawah ini merupakan jajargenjang ABCD dengan sisi-sisi AB, BC, CD, dan DA, serta DE merupakan tingginya. Keliling jajargenjang ABCD = AB + BC + CD + AD.

Jajargenjang ABCD

Oleh karena AB = DC dan AD = BC, maka keliling jajargenjang
= AB + DC + BC + AD
= AB + AB + BC + BC
= 2AB + 2BC
= 2 (AB + BC)

(a) Jajargenjang ABCD dengan AB = a dan BC = b, (b) jajargenjang
ABCD dengan t sebagai tinggi.

Gambar diatas (a) merupakan jajargenjang dengan sisi-sisinya, yaitu a dan b.

Keliling jajargenjang adalah 2a + 2b = 2 (a + b)

Untuk menentukan luas jajargenjang, coba lakukan kegiatan berikut.

1. Buatlah jajargenjang ABCD, lalu buatlah garis tinggi DE dari titik D ke garis AB.
2. Guntinglah jajargenjang tadi sepanjang garis tingginya. Lalu gabungkan lagi sehingga terbentuk persegi panjang.

Luas jajargenjang ABCD = luas persegi panjang
= alas · t
= AB · DE

Dari uraian di atas dapat kita simpulkan jika AB disebut alas dan DE disebut tinggi jajargenjang, maka

luas jajargenjang = alas × t

Contoh Soal:

ABCD adalah jajargenjang dengan AB = 10 cm, BC = 8 cm, dan DE = 6 cm. Tentukanlah luas jajargenjang tersebut.

Penyelesaian:
Luas jajargenjang = alas × tinggi
= 10 cm × 6 cm

= 60 cm²

 

^{sumber: http://www.plengdut.com/2013/03/keliling-dan-luas-jajargenjang.html} 

Keliling dan Luas Belah Ketupat

Pada Gambar dibawah ini (a), ABCD adalah belah ketupat. Keliling belah ketupat pada Gambar (a) adalah AB + BC + CD + DA. Sisi-sisi belah ketupat sama panjang, yaitu AB = BC = CD = DA.

(a) Belah ketupat ABCD (b) belah
ketupat ABCD dan persegi
panjang EFGH

Keliling belah ketupat = 4 × sisi = 4s

Pada Gambar (b), ABCD adalah belah ketupat dan EFGH adalah persegi panjang dengan panjang EF = AC = HG dan EH = BD = GF.

Luas persegi panjang EFGH = EF × FG.

Luas belah ketupat ABCD = ½ luas persegi panjang EFGH
= ½ × EF × FG
= ½ × AC × BD

AC dan BD merupakan diagonal-diagonal belah ketupat, maka luas belah ketupat ABCD dapat ditulis sebagai berikut.

Luas belah ketupat ABCD = ½ × d₁ × d₂

Contoh Soal: 
Diagonal-diagonal sebuah belah ketupat adalah 12 cm dan 8 cm. Hitunglah luas belah ketupat tersebut.

Penyelesaian:
Luas = ½ x 12cm x 8cm = 48cm²

 

 

^{sumber: http://www.plengdut.com/2013/03/keliling-dan-luas-belah-ketupat.html} 

Keliling dan Luas layang-Layang

Pada Gambar berikut, ABCD adalah layang-layang. Pada layang-layang ABCD sepasang sisi-sisinya sama panjang, yaitu DA = DC dan BA = BC.

Keliling layang-layang ABCD = AB + BC + CD + DA
= 2AB + 2AD
= 2 (AB + AD)

Layang-layang ABCD

Keliling layang-layang sama dengan jumlah sisi-sisi layang-layang

Pada Gambar dibawah ini, ABCD adalah layang-layang dengan diagonal AC dan BD saling tegak lurus. EFGH adalah persegi panjang dengan panjang EF = HG = AC dan EH = FG = BD.

Layang-layang ABCD dan persegi panjang
EFGH

Luas persegi panjang = EF × EH
Luas layang-layang = ½ × luas persegi panjang
= ½ × EF × EH
= ½ × AC × BD
= ½ × diagonal₍₁₎ × diagonal₍₂₎
= ½ × d₁ × d₂

Luas layang-layang = ½ × d₁ × d₂

Contoh Soal:

ABCD adalah layang-layang dengan AE = 4 cm dan BD = 24 cm. Hitunglah luas ABCD.

Penyelesaian:
Luas ABCD = ½ (AC x BD)
= ½ (8 x 24) = 96 cm²

Jadi luas ABCD adalah 96 cm².

 

 

sumber:  http://www.plengdut.com/2013/03/keliling-dan-luas-layang-layang.html

Sifat Layang-Layang

ayang-layang memiliki sifat-sifat sebagai berikut.

a. Sisinya Sepasang-sepasang Sama Panjang

Layang-layang dibentuk oleh dua segitiga sama kaki yang memiliki luas berbeda dan alasnya sama panjang berimpit. Perhatikanlah segitiga-segitiga pada layang-layang ABCD. Segitiga ACD adalah sama kaki dengan alas AC, maka AD = DC. Begitu juga segitiga sama kaki ABC dengan alas AC, maka AB = BC, sehingga layang-layang ABCD mempunyai sisi sepasang-sepasang yang sama panjang, yaitu CD = AD dan AB = BC.

Sepasang-sepasang sisi pada layang-layang adalah sama panjang.

Sisi-sisi pada
layang-layang DA = DC,
BA = BC

b. Sepasang Sudut yang Berhadapan Sama Besar

Perhatikanlah layang-layang ABCD pada Gambar dibawah ini. Segitiga ABC adalah segitiga sama kaki dengan ∠BAC = ∠BCA = y°. Segitiga ADC adalah segitiga sama kaki dengan ∠DAC = ∠DCA = x°.

Layang-layang ABCD dibentuk dari dua segitiga sama kaki, yaitu segitiga sama kaki ADC dan ABC, maka:

 ∠DAB = ∠CAB + ∠DAC = yº + xº
∠BCD = ∠BCA + ∠ACD = yº + xº

Dari uraian di atas dapat dikatakan bahwa ∠BAD = ∠BCD.

Sepasang sudut pada layang-layang adalah sama besar

Sudut-sudut pada
layang-layang ∠BAD = ∠BCD

c. Salah Satu Diagonal adalah Sumbu Simetri

Perhatikanlah layang-layang ABCD pada Gambar dibawah ini. Pada layang-layang ABCD sisinya sepasang-sepasang sama panjang, yaitu AB = BC dan AD = DC. Serta sepasang sudut yang berhadapan sama besar, yaitu ∠DAB = ∠BCD.

Tariklah garis dari B ke D, maka akan terbentuk dua segitiga yang kongruen yaitu ∠DAC dan ∠BCD yang berimpit di BD. Karena BD membagi layang-layang ABCD menjadi dua segitiga yang kongruen, maka BD adalah sumbu simetri. Sumbu simetri adalah garis yang membagi bidang datar menjadi dua bagian yang kongruen (sama besar). Pada Gambar, BD merupakan sumbu simetri.

Salah satu diagonal layang-layang merupakan sumbu simetri layang-layang

Diagonal BD
merupakan sumbu simetri
pada layang-layang

d. Salah Satu Diagonalnya Membagi Dua Sama Panjang dan Tegak Lurus Diagonal Lainnya

Garis BD membagi layang-layang ABCD menjadi dua segitiga yang kongruen yaitu ΔABD dan ΔBCD. Sisi-sisi yang berdekatan sama, yaitu AD = DC dan AB = BC, maka diagonal BD membagi AC menjadi sama panjang dan BD ⊥ AC. Oleh karena yang menjadi cermin adalah BD, maka BD tidak pindah (tetap) dan ⊥ AC. Pada keadaan demikian, BD disebut garis invarian.

BD membagi AC menjadi dua bagian yang sama panjang, yaitu AE = EC dan BD tegak lurus AC.

Salah satu diagonal layang-layang membagi dua sama panjang dan tegak lurus diagonal lainnya

Diagonal diagonal pada layang-layang
saling tegak lurus

Contoh Soal:

Sebuah layang-layang ABCD dengan diagonal panjang BD. Jika ∠D = 108° dan ∠DAC = 3x, dan ∠ACB = 5x, tentukanlah:

a. ∠DCA                      b. ∠DAB

Penyelesaian:
a. Perhatikanlah ΔACD
∠D + ∠DAC + ∠ACD = 180°
108° + 3x + 3x = 180°
6x = 180° – 108°

6x = 72°
x = 12°
∠DCA = ∠DAC = 3x
= 3(12°) = 36°

b. ∠DAB = 3x + 5x
= 8x
= 8 (12)°
= 96°

Komplemen

Komplemen dari himpunan A adalah himpunan yang anggota-anggotanya bukan merupakan anggota himpunan A.

Contoh: S = {0, 1, 2, 3, 4, 5, 6, 7}
A = {2, 3, 4, 5}

Komplemen dari himpunan A adalah {0, 1, 6, 7}. Komplemen dari himpunan A dapat dinotasikan atau ditulis A' dibaca A komplemen atau komplemen dari A. Komplemen A juga dapat dinyatakan dengan diagram Venn. Diagram Venn dari A' dinyatakan seperti Gambar berikut ini.

Komplemen A

Contoh Soal:

1. Perhatikan diagram Venn berikut ini.

 

Tentukan:
a. S        c. B         e. A' ∩ B
b. A       d. A'

Penyelesaian:
a. S = {1, 2, 3, 4, 5, 6, 7, 8, 9}
b. A = {1, 2, 3, 4, 5}
c. B = {5, 6, 7}
d. A' = {6, 7, 8, 9}
e. A' ∩ B = {6, 7}
 

2. Perhatikan diagram Venn berikut ini.

Tentukan:
a. A'         d. A' ∩ B      g. B' ∩ A
b. B'         e. A' ∩ C      h. C' ∩ B
c. C'         f. B' ∩ C       i. C' ∩ A

Penyelesaian:
a. A' = {4, 5, 6, 8, 11, 12, 13, 14, 15]
b. B' = {1, 2, 3, 10, 11, 12, 13, 14, 15}
c. C' = {1, 2, 3, 4, 5, 6, 7, 13, 14, 15}
d. A' ∩ B = {4, 5, 6, 8}
e. A' ∩ C = {8, 11, 12}
f. B' ∩ C = {10, 11, 12}
g. B' ∩ A = {1, 2, 3, 10}
h. C' ∩ B = {4, 5, 6, 7}
i. C' ∩ A = {1, 2, 3, 7}

 

Sumber: http://www.plengdut.com/2013/03/komplemen.html

Keliling dan Luas Persegi dan Persegi Panjang

Gambar berikut ini menunjukkan sebuah persegi. Pada gambar persegi di samping keempat sisinya sama panjang, yaitu sisi AB = BC = CD = DA. Jadi, keliling dan luas persegi dapat dituliskan sebagai berikut.

Persegi ABCD

Keliling persegi = 4 × sisi = 4s
Luas persegi = sisi × sisi = s²

 

 

 

Pada Gambar dibawah ini, ABCD adalah persegi panjang. Keliling persegi panjang tersebut adalah AB + BC + CD + AD. Oleh karena AB = DC dan AD = BC, maka:

keliling persegi panjang ABCD = AB + DC + BC + AD
= 2AB + 2BC
= 2 (AB + BC)
(AB disebut panjang dan BC disebut lebar)

Persegi panjang ABCD

Keliling persegi panjang = 2p + 2l = 2 (p + l)
Luas persegi panjang = AB × BC = p x l

sumber: http://www.plengdut.com/2013/03/keliling-dan-luas

Keliling dan Luas Segitiga

Pada bagian sebelumnya kalian telah mempelajari segitiga ditinjau dari panjang sisi-sisinya dan besar sudut-sudutnya, bukan? Di samping dua hal tersebut, pada suatu segitiga ada hal lain yang sangat menarik untuk dipelajari. Dapatkah kalian menerka apakah itu? Ya, kalian benar di samping sisi-sisi dan sudut-sudut pada suatu segitiga, keliling dan luas dari suatu segitiga merupakan dua permasalahan yang sangat penting untuk kalian kuasai dengan baik. Agar kalian lebih paham, simak baikbaik uraian berikut.

Keliling Segitiga

Keliling segitiga adalah jumlah panjang semua sisi-sisi segitiga tersebut. Pada Gambar berikut ini, keliling ΔABC adalah AB + BC + AC.

Segitiga ABC

Jadi:

keliling Δ ABC = a + b + c

Contoh Soal:

Pada gambar di bawah ini, panjang AB = 10 cm, BC = 8 cm, dan AC = 9 cm. Hitunglah keliling segitiga itu?

Penyelesaian:
Keliling Δ ABC = AB + BC + AC
= 10 + 8 + 9
= 27 cm

Luas Segitiga

Pada penjelasan sebelumnya telah dijelaskan bahwa segitiga memiliki tiga sisi dan tiga sudut. Setiap sisi pada segitiga dapat merupakan alas dari segitiga tersebut. Pada Gambar berikut ini, Δ ABC dengan alas:

AB memiliki tinggi CE
AC memiliki tinggi BD
BC memiliki tinggi AF

Segitiga ABC

Hasil kali alas dan tinggi kemudian dibagi dua merupakan luas segitiga.

Pada Gambar berikut ini, Δ ABC mempunyai:

alas AB dan tinggi CF
alas AC dan tinggi BD
alas BC dan tinggi AE

 

Segitiga ABC

 

Hasil kali alas dan tinggi kemudian dibagi dua merupakan luas segitiga.

Luas Δ ABC = Luas segitiga = ½ (alas x tinggi)

Luas segitiga = ½ (a x t)

Contoh soal:

Hitunglah luas segitiga pada gambar di bawah ini.

Penyelesaian:
a. Luas Δ ABC = ½ (18cm x 12cm) = 108 cm²

b. Luas Δ PQR = ½ (10cm x 9cm) = 45 cm²

 

sumber: http://www.plengdut.com/2013/03/besaran-besaran-pada-segitiga.html

Operasi Kurang pada Himpunan

Selisih dari himpunan A dan himpunan B adalah jumlah seluruh anggota A yang bukan anggota B.

Contoh: A = {1, 2, 3, 4}
B = {2, 3}
Selisih himpunan A dan B adalah {1, 4}.

Selisih himpunan A dan B dapat dinotasikan atau ditulis A – B. Selisih himpunan A dan B juga dapat dinyatakan dengan diagram Venn. A – B ditunjukkan dengan diagram Venn seperti Gambar dibawah ini. Perhatikan bahwa daerah yang diarsir adalah selisih A – B.

Selisih A–B

 

 

 

sumber: http://www.plengdut.com/2013/03/selisih.html

Glosarium

 1.1  Konsep Himpunan

Konsep himpunan merupakan konsep dasar dalam matematika.

Definisi :

Himpunan adalah koleksi obyek yang didefinisikan secara jelas dalam sembarang urutan.

Cara mengoleksi obyek-obyek dapat didasarkan pada sifat mereka yang sama atau berdasarkan suatu aturan tertentu. Obyek-obyek yang menjadi anggota dari himpunan ini disebut dengan elemen dari himpunan tersebut. Jika p anggota himpunan A, ditulis pÎA, dibaca ‘p adalah elemen (anggota) dari himpunan A’. Jika obyek q bukan anggota dari himpunan A, ditulis qÏA.

 1.2  Notasi dan Definisi

Himpunan dinyatakan dengan huruf besar : A, B, C,…, sedangkan elemen-elemennya dinyatakan dengan huruf kecil : a, b, c, …..

Contoh :

1. Himpunan A terdiri atas bilangan 1,3,5,7, maka dapat dituliskan sebagai A = {1,3,5,7}
2. Himpunan B adalah himpunan bilangan genap positif, maka dapat dituliskan dalam bentuk : B = {xïx genap >0}

 Terdapat tiga cara penulisan himpunan yaitu :

1. Dengan mendaftar anggota-anggotanya .

Contoh :

X = {2, 3, 5, 7, 11}

Y = {a, b, c, d}

2. Dengan menyatakan sifat-sifat yang dipenuhi oleh anggota-anggotanya

X = Himpunan 5 bilangan prima yang pertama}

Y = Himpunan 4 abjad huruf kecil yang pertama}

3. Dengan menggunakan notasi pembentuk himpunan.

X = {x½0< x < 13, x Î bilangan prima}

Y = {x½x Î 4 abjad huruf kecil yang pertama}

Definsi-Definisi pada teori himpunan :
a.    Himpunan Semeseta

Himpunan semesta adalah himpunan yang anggotanya semua obyek yang sedang dibicarakan, dinotasikan dengan S atau U.

Contoh :

• Semesta pembicaraan dari himpunan A = {a,b,c,d} dan B={c,d,e,f} adalah S = himpunan huruf-huruf  kecil.
•  Semesta pembicaraan dari himpunan A = {2,5,7} adalah S = {1,3,5,7,9}

b.     Himpunan Kosong

Himpunan kosong adalah himpunan yang tidak mempunyai anggota yang dinotasikan dengan { } atau f.

Contoh :

A = {x½x²=-1, xÎbilangan asli}, maka P = {}

 c.      Himpunan kuasa (Power Set)

Himpunan kuasa adalah himpunan seluruh himpunan bagian dari suatu himpunan.

Contoh :

Himpunan bagian dari himpunan A = {1,2,3} adalah { },{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}.

Banyaknya himpunan bagian dari dari suatu himpunan yang beranggotakan n anggota adalah 2ⁿ himpunan bagian.

 d.     Himpunan Berhingga (finite) dan Himpunan Tak Berhingga (infinite)

Himpunan berhingga adalah suatu himpunan yang elemennya berbeda yang banyaknya tertentu.

Himpunan tak berhingga adalah suatu himpunan yang elemennya berbeda yang banyaknya tidak tertentu.

Contoh :

P = himpunan bilangan prima, maka infinite

Q = himpunan bilangan prima kurang dari 10, maka Q finite.

1.3  Operasi-operasi Himpunan
a.      Union (Gabungan) Himpunan

Union himpunan A dan himpunan B adalah himpunan dari semua elemen yang termasuk dalam A atau B atau keduanya yang dinyatakan dengan simbol Ù.

Pernyataan tersebut dapat ditulis sebagai berikut :

A Ù B ={xεA atau xεB}.

Contoh :

A = {a,b,c,d} dan B={c,d,e,f}, maka A Ù B = {a,b,c,d,e,f}

 b.       Interseksi (Irisan) Himpunan

Interseksi himpunan A dan himpunan B adalah himpunan dari elemen-elemen yang termasuk dalam himpunan A maupun B, yang dinyatakan dengan simbol ∩.

Pernyataan tersebut dapat ditulis sebagai berikut :

A ∩ B ={x elemen A dan x  elemenB}.

Contoh :

A = {a,b,c,d} dan B={c,d,e,f}, maka A ∩ B = {c,d}

 c.   Selisih Himpunan

Selisih himpunan A dan himpunan B adalah himpunan dari elemen-elemen yang termasuk A tetapi tidak termasuk B, dinyatakan dengan :

A – B = {x elemen A dan x bukan elemenB}.

Contoh :
A = {a,b,c,d} dan B={c,d,e,f}, maka A – B = {a,b}
d.       Jumlah Himpunan

Jumlah himpunan A dan himpunan B adalah himpunan dari elemen-elemen yang termasuk A atau B tetapi tidak termasuk keduanya, dinyatakan dengan :

A + B = { x elemen A, x elemen b dan x bukan elemen A ∩ B}.

Contoh :

A = {a,b,c,d} dan B={c,d,e,f}, maka A + B = {a,b,e,f}

e.  Komplemen Himpunan

Komplemen dari himpunan A adalah himpunan dari elemen-elemen yang tidak termasuk A tetapi masih dalam semesta pembicaraanS. Secaramatematis ditulis

Pernyataan tersebut dapat ditulis sebagai berikut :

A’ = { x elemen S dan x bukan elemen A}

Contoh :

A = {b,c,d} dan S={a,b,c,d,e,f}, maka A’ = {a,e,f}

f. Himpunan Bagian

Himpunan A disebut himpunan bagian dari himpunan B jika setiap anggota A juga merupakan anggota B, ditulis A C B.

Contoh :

A = {b,c,d} dan B={a,b,c,d,e,f}, maka A  C B

g.      Himpunan Sama

Himpunan A disebut sama dengan himpunan B jika A Ì B dan B Ì A.

Contoh :

A = {b,c,d} dan B={b,c,d}, maka A = B

sumber: http://wawanlaksito.wordpress.com/2011/05/20/teori-himpunan/

Cara Menyatakan Himpunan

Cara Menyatakan Himpunan
Misalkan diketahui himpunan lima abjad yang pertama adalah a, b, c, d, dan e. Jika kelima abjad yang pertama ini dinyatakan dalam himpunan, maka himpunan itu harus diberi nama terlebih dahulu. Nama himpunan biasa ditulis dengan huruf kapital. Himpunan lima abjad yang pertama dapat ditulis sebagai berikut.

 

A = {a, b, c, d, e}

Di samping menyatakan suatu himpunan seperti pada contoh di atas, adakah cara lain untuk menyatakannya? Pada dasarnya ada tiga cara untuk menyatakan himpunan yaitu:

• menyatakan dengan kata-kata;
• mendaftar (tabulasi);
• notasi.

1) Cara Menyatakan Himpunan dengan kata-kata
Untuk menyatakan a, b, c, d, dan e sebagai himpunan dengan kata-kata adalah sebagai berikut.
 

A = himpunan lima abjad pertama

Untuk menuliskan 1, 2, 3, 4, dan 5 sebagai himpunan dengan kata-kata sebagai berikut.

B = himpunan lima bilangan asli yang pertama,

atau dapat ditulis

B = himpunan bilangan asli yang kurang dari 6.

2) Cara Menyatakan Himpunan dengan Mendaftar (Tabulasi)
Cara menyatakan himpunan dengan mendaftar dilakukan dengan menuliskan anggota dari himpunan tersebut. Semua anggota himpunan ditulis dalam tanda kurung kurawal dan penyebutan anggota yang satu dengan yang lain dipisahkan dengan tanda koma. Perhatikan contoh berikut ini.

a) A = {2, 3, 5, 7, 9}
b) M = {Bandung, Jakarta, Semarang, Surabaya}
c) S = {Senin, Selasa, Sabtu}
d) C = {1, 2, 3, 4, ...}

Menyatakan himpunan dengan cara seperti ini sangat cocok untuk himpunan yang jumlah anggotanya sedikit. Ada tiga hal yang perlu kalian perhatikan dalam menyatakan himpunan dengan cara mendaftar, yaitu sebagai berikut.

a) Anggota suatu himpunan yang muncul lebih dari satu kali, cukup ditulis sekali saja.
b) Penulisan anggota himpunan boleh mengabaikan urutannya.
c) Untuk himpunan yang jumlah anggotanya tak terhingga dan anggotanya mempunyai urutan tertentu dapat menggunakan tanda tiga titik (...).

3) Cara Menyatakan Himpunan dengan Menggunakan Notasi
Himpunan yang dinyatakan dengan cara ini tidak disebutkan anggota-anggotanya. Yang disebutkan hanyalah
syarat atau aturan yang harus dipenuhi oleh suatu objek agar dapat menjadi anggota himpunan yang bersangkutan. Penyajian himpunan dengan cara ini dinamakan menggunakan notasi pembentuk himpunan. Penulisan dengan notasi pembentuk himpunan dinyatakan sebagai berikut.
 

A = {x|...., x ∈ ....}

 

Misalkan diketahui A = {1, 2, 3, 4, 5}. Himpunan A dapat dinamakan sebagai himpunan lima bilangan asli pertama. Dengan cara notasi pembentuk himpunan ditulis dalam bentuk:

A = {x|x < 6, x ∈ bilangan asli}

Penotasian tersebut dibaca sebagai himpunan A dengan x kurang dari 6 dan x anggota bilangan asli. Selain penyataan himpunan dengan cara notasi seperti di atas, ada pula cara penotasian yang berbentuk sebagai berikut.

A = {(x, y)| .... , x, y ∈ bilangan ....}

Contoh:
A = {(1, 1), (2, 2), (3, 3), (4, 4), ....} dapat dinyatakan dalam bentuk notasi sebagai berikut.

A = {(x, y)|x = y; x, y ∈ bilangan asli}

sumber: http://www.plengdut.com/2013/03/himpunan-bilangan-bilangan.html

Sifat-Sifat Jajar Genjang

Agar kalian lebih memahami sifat-sifat jajargenjang, lakukan kegiatan berikut ini.
 

a. Jiplaklah segitiga ABD pada Gambar dibawah ini lalu buatlah titik O di tengah-tengah BD. 

Segitiga ABD

Putarlah segitiga ABD sebesar 180° dengan pusat O, kemudian amati bangun hasil putaran tersebut. Apakah hasilnya seperti bangun jajargenjang pada Gambar dibawah ini?

Segi empat ABCD hasil perputaran
segitiga ADB di O

A → C               AB = DC dan ∠A = ∠C
B → …              AD = … dan ∠B = ∠…
sehingga terdapat dua ruas garis yang sejajar, yaitu
 

AD // … dan DC // ....
 

Dengan demikian, dapat disimpulkan pada setiap jajargenjang berlaku sifat-sifat berikut.

• sisi-sisi yang … sejajar
• sisi-sisi yang … sama panjang, dan
• pada setiap jajargenjang, sudut-sudut yang … sama besar.

b. Buatlah garis AO. Jika segitiga ABD diputar 180º dengan pusat O, apakah hasilnya seperti pada Gambar dibawah ini? Dengan demikian:

AO berimpit dengan OC sehingga AO = OC
BO berimpit dengan … sehingga BO = …

 

sumber: www.plengdut.com/2013/03/sifat-sifat-jajargenjang.html

SIFAT-SIFAT SEGITIGA

SIFAT-SIFAT SEGITIGA

1. Segitiga Siku-Siku

Segitiga siku-siku dapat dibentuk dari sebuah persegi panjang dengan menarik salah satu garis diagonalnya.

Perhatikan gambar berikut:

Bidang ABCD adalah persegi panjang. Dengan menarik diagonal AC, akan terbentuk dua segitiga siku-siku yang sama dan sebangun (konruen) yaitu ΔABC dan ΔADC.

Segitiga siku-siku mempunyai dua sisi siku-siku yang mengapit sudut siku-siku dan satu sisi miring (hypotenusa)

ΔABC mempunyai ciri-ciri:

AB dan BC sebagai sisi siku-siku, AC sebagai hypotenusa dan sudut ABC atau sudut B adalah sudut siku-siku (= 90°)

Dalam sebuah segitiga siku-siku, hypotenusa selalu terletak di depan sudut siku-siku.

2. Segitiga Sama Kaki

Dua buah segitiga siku-siku yang kongruen dapat membentuk sebuah segitiga sama kaki dengan mengimpitkan salah satu sisi siku-siku yang sama panjang dari kedua segitiga tersebut.

Perhatikan gambar berikut:

ΔABD dan ΔDBC adalah dua segitiga siku-siku yang kongruen. Sisi BD adalah sisi siku-siku yang sama panjang dari kedua segitiga tersebut. Jadi ΔACD adalah segitiga sama kaki dengan sisi AD=DC.

Di dalam segitiga sama kaki terdapat :

• Dua sisi yang sama panjang, sisi tersebut sering disebut kaki segitiga.
• Dua sudut yang sama besar yaitu sudut yang berhadapan dengan sisi yang panjangnya sama.
• Satu sumbu simetri.

Segitiga sama kaki merupakan bangun simetri lipat dan dapat menempati bingkainya dalam dua cara.

Dari gambar disamping terlihat bahwa :

1. CD sebagai sumbu simetri
2. A pindah ke B; B pindah ke A dan C tetap.
3. AC pindah ke BC, maka AC=BC.
4. CAB pindah ke  ABC maka  CAB =  ABC

3. Segitiga Sama Sisi

Tiga buah garis lurus yang sama panjang dapt membentuk sebuah segitiga sama sisi dengan cara mempertemukan setiap ujung garis satu sama lainnya.

Gambar (i) di atas menunjukkan gambar tiga garis lurus yang sama panjang, yaitu AB= BC=CA. Apabila ujung-ujung ketiga garis tersebut saling dipertemukan, A dengan A, B dengan B, dan C dengan C, maka akan terbentuk segitiga sama sisi ABC seperti terlihat pada gambar (ii) di atas

Di dalam segitiga sama sisi terdapat :

1. Tiga sisi yang sama panjang.
2. Tiga sudut yang sama besar.
3. Tiga sumbu simetri.

sumber:http://segitigasmp.wordpress.com/sifat-sifat-segitiga/

Irisan Himpunan

Irisan dari dua himpunan A dan B adalah himpunan yang anggota-anggotanya ada di himpunan A dan ada di himpunan B. Dengan kata lain, himpunan yang anggotanya ada di kedua himpunan tersebut.

Contoh: A = {a, b, c, d, e} dan B = {b, c, f, g, h}

Pada kedua himpunan tersebut ada dua anggota yang sama yaitu b dan c. Oleh karena itu, dapat dikatakan bahwa irisan himpunan A dan B adalah b dan c atau ditulis dengan:

A ∩ B = {b, c}

A ∩ B dibaca himpunan A irisan himpunan B. Dengan diagram Venn A ∩ B dapat dinyatakan seperti pada Gambar berikut ini.

Daerah irisan A dan B.

Contoh Soal:

1. Diketahui: A= {1, 2, 3, 4, 5}
B = {2, 3, 6, 7, 8}
C = {4, 5, 6, 7, 8}
Tentukanlah:
a. A ∩ B         c. B ∩ C
b. A ∩ C        d. A ∩ B ∩ C

Penyelesaian:
a. A ∩ B = {2, 3}       c. B ∩ C = {6, 7, 8}
b. A ∩ C = {4, 5}      d. A ∩ B ∩ C = { }

2. Perhatikan gambar berikut.

Tentukanlah:
a. A                 e. n(A)
b. B                 f. n(B)
c. A ∩ B         g. n(A ∩ B)
d. S                 h. n(S)

 Penyelesaian:
a. A = {1, 2, 3, 4, 5}
b. B = {4, 5, 6, 7, 8}
c. A ∩ B = {4, 5}
d. S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
e. n(A) = 5

f. n(B) = 5
g. n(A ∩ B) = 2
h. n(S) = 11

sumber: http://www.plengdut.com/2013/03/